Page 57 - Zmist-n2-2015

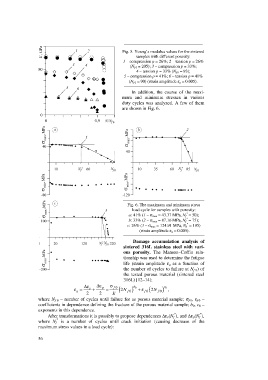
Fig. 5. Young’s modulus values for the sintered
samples with different porosity:
1 – compression p = 26%; 2 – tension p = 26%
(N f 0 = 205); 3 – compression p = 33%;
4 – tension p = 33% (N f 0 = 93);
5 – compression p = 41%; 6 – tension p = 41%
(N f 0 = 90) (strain amplitude e a = 0.005).

In addition, the course of the maxi-
mum and minimum stresses in various
duty cycles was analyzed. A few of them
are shown in Fig. 6.

Fig. 6. The maximum and minimum stress
load cycle for samples with porosity:
*
a: 41% (1 – s max = 43.37 MPa, N f = 50);
*
b: 33% (2 – s max = 87.16 MPa, N f = 75);
*
c: 26% (3 – s max = 124.91 MPa, N f = 195)
(strain amplitude e a = 0.005).
Damage accumulation analysis of
sintered 316L stainless steel with vari-
ous porosity. The Manson–Coffin rela-
tionship was used to determine the fatigue
life (strain amplitude e a as a function of
the number of cycles to failure at N f 0) of
the tested porous material (sintered steel
316L) [12–14]:
De e De p s 0 b 0 c 0
f
e = + = ( 2N f 0 ) + e 2N ) ,
a
0
f
( 0f
2 2 E
where N f 0 – number of cycles until failure for as porous material sample; s f 0, e f 0 –
coefficients in dependence defining the fracture of the porous material sample; b 0, c 0 –
exponents in this dependence.
* *
After transformations it is possibly to propose dependences ∆e e(N f ), and ∆e p(N f ),
*
where N f is a number of cycles until crack initiation (causing decrease of the
maximum stress values in a load cycle):
56