Page 43 - Zmist-n3-2015-new

де s f – міцність волокон; l c – гранична неефективна довжина волокна; l – довжи-
на волокна; l – коефіцієнт приведення хаотичного армування до напрямленого [1]
(l = 1 – для напрямленого армування вздовж осі розтягу; l = 0,33 – для хаотичного).
Встановлення величини l c в
точній постановці є досить склад-
ною задачею теорії пружності. Ра-
ніше наведено [12] достатньо гро-
міздкий вираз для обчислення l c,
отриманий наближеним методом. У
механіці композитів використову-
ють припущення, що дотичні на-
пруження t на циліндричній по-
верхні волокна є сталими і з рів-
няння його рівноваги отримують
просту залежність
Рис. 3. Схема армованого цементного каменю s f r ×
з порами: 1 – пори; 2 – тріщини; l = , (5)
c
3 – мікроволокна. t
де r – радіус волокна. Враховуючи
Fig. 3. Scheme of reinforced cement with pores:
1 – pores; 2 – cracks; 3 – microfiber. залежності (3), (4), отримуємо роз-
рахункову формулу для прогнозу-
вання міцності волокнистого ком-
позита (фібробетону) на основі цементної матриці

f  a    l  
c
) .
(1 V-
R =  1 -   ls V f  1 -  + s f  (6)
bt f 0
 d    2l  
f
Наведені (рис. 4–6) графічні залежності міцності матеріалів R від об’ємного
bt
вмісту волокон базальту, поліпропілену, скла та вуглецю і пошкоджень у цемент-
ній матриці. Механічні характеристики волокон наведені у табл. 1.

f
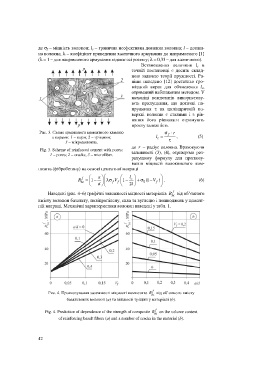
Рис. 4. Прогнозування залежності міцності композита R від об’ємного вмісту
bt
базальтових волокон (а) та кількості тріщин у матеріалі (b).

f
Fig. 4. Prediction of dependence of the strength of composite R on the volume content
bt
of reinforcing basalt fibers (а) and a number of cracks in the material (b).

42