Page 98 - Zmist-n2-2015

Венана. Криві 6, 7 описують границю текучості ненаводнених та наводнених
зразків за критерієм Губера–Мізеса:
2
2
2
s + s - s s = s. (2)
z q z q Т
Отже, для розрахунків граничного стану текучості можна використовувати
рівняння Губера–Мізеса. Характерним під час пропорційного навантаження зраз-
ка є незмінність жорсткості НС як за досягнення текучості, так і міцності (табл. 2
і рис. 4).
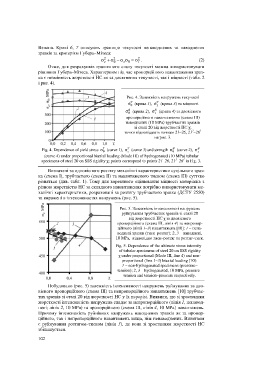
Рис. 4. Залежність напружень текучості
T
T
s (крива 1), s (крива 3) та міцності
z
q
B
B
s (крива 2), s (крива 4) за двовісного
z
q
пропорційного навантаження (схема ІІІ)
наводнених (10 МРа) трубчастих зразків
зі сталі 20 від жорсткості НС χ;
1 1
точки відповідають точкам 21–26, 21 –26
на рис. 3.

T
T
B
B
Fig. 4. Dependence of yield stress s (curve 1), s (curve 3) and strength s (curve 2), s
q
q
z
z
(curve 4) under proportional biaxial loading (Mode III) of hydrogenated (10 MPa) tubular
1
1
specimens of steel 20 on SSS rigidity χ; points correspond to points 21–26, 21 –26 in Fig. 3.
Визначені за одновісного розтягу механічні характеристики суцільного зраз-
ка (схема І), трубчастого (схема ІІ) та навантаженого тиском (схема ІІІ) суттєво
різняться (див. табл. 1). Тому для коректного оцінювання міцності матеріалів з
різною жорсткістю НС за складного навантаження потрібно використовувати ме-
ханічні характеристики, розраховані за розтягу трубчастого зразка (ДСТУ 2550)
та виражені в інтенсивностях напружень (рис. 5).
Рис. 5. Залежність інтенсивності напружень
руйнування трубчастих зразків зі сталі 20
від жорсткості НС χ за двовісного
пропорційного (схема ІІІ, лінія 4) та непропор-
ційного (лінії 1–3) навантажень [10]: 1 – нена-
воднені зразки (тиск–розтяг); 2, 3 – наводнені,
10 МРа, відповідно тиск–розтяг та розтяг–тиск.
Fig. 5. Dependence of the ultimate stress intensity
of tubular specimens of steel 20 on SSS rigidity
χ under proportional (Mode III, line 4) and non-
proportional (line 1–3) biaxial loading [10]:
1 – non-hydrogenated specimens (pressure–
tension); 2, 3 – hydrogenated, 10 MPa, pressure–
tension and tension–pressure respectively.

Побудовано (рис. 5) залежність інтенсивності напружень руйнування за дво-
вісного пропорційного (cхема ІІІ) та непропорційного навантажень [10] трубчас-
тих зразків зі сталі 20 від жорсткості НС у їх перерізі. Виявили, що зі зростанням
жорсткості інтенсивність напружень спадає за непропорційного (лінія 1, ненавод-
нені; лінія 2, 10 МРа) та пропорційного (схема ІІІ, лінія 4, 10 МРа) навантажень.
Причому інтенсивність руйнівних напружень наводнених зразків як за пропор-
ційного, так і непропорційного навантажень вища, ніж ненаводнених. Винятком
є руйнування розтягом–тиском (лінія 3), де вона зі зростанням жорсткості НС
збільшується.
102