Page 28 - Zmist-n3-2015-new

4. Нехай тріщина залікована на багатьох дрібних ділянках завдовжки d - 2l
з кроком d = 2 /l 0 N (N – кількість ділянок). Тоді y = 1 2 /l d- .
Прийнявши за великих N справедливими результати періодичної задачі
[7, 8], отримаємо:
2Eg h l p
p » ctg . (7)
h
d d
Як наслідок співвідношень (3), (8)
p N py
c » h tg . (8)
2 2
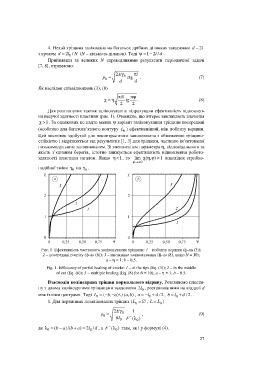
Для розглянутих тактик заліковування підрахували ефективність відновлен-
ня несучої здатності пластини (рис. 1). Очевидно, що інтерес викликають значення
c 1 > . За однакових не надто малих y варіант заліковування тріщини посередині
(особливо для багатозв’язного контуру L ) ефективніший, ніж поблизу вершин.
h
Цей висновок здобутий для неконтрастного заповнювача з обмеженою тріщино-
стійкістю і відрізняється від результатів [1, 3] для тріщини, частково ін’єктованої
низькомодульним заповнювачем. Зі зменшенням параметра h, відповідального за
якість з’єднання берегів, істотно знижується ефективність відновлення робото-
здатності пластини загалом. Якщо h< , то lim c ( , ) 1h j ¹ внаслідок стрибко-
1
j®+ 0
подібної зміни g на g .
h
0

Рис. 1. Ефективність часткового заліковування тріщини: 1 – поблизу вершин (ф-ла (3));
2 – посередині розрізу (ф-ла (6)); 3 – множинне заліковування (ф-ла (8), якщо N = 10);
а – h = 1; b – 0,5.
Fig. 1. Efficiency of partial healing of cracks: 1 – at the tips (Eq. (3)); 2 – in the middle
of cut (Eq. (6)); 3 – multiple healing (Eq. (8) for N = 10); а – h = 1; b – 0.5.

Взаємодія колінеарних тріщин нормального відриву. Розглянемо пласти-
ну з двома колінеарними тріщинами завдовжки 2l , розташованими на віддалі d
0
між їхніми центрами. Тоді L = ( b a- - ) È ( , )a b , a = - + /2 , b l= 0 + d /2 .
d
l
,
0
0
1. Для первинних незалікованих тріщин (L = Æ, L = L )
h
0
2Eg 0 1
p = , (9)
0
l p 0 F - (l 0 )
-
де l = (b a- )/(b a+ ) 2 /l= 0 d , а F (l таке, як і у формулі (4).
)
0
0
27