Page 29 - Zmist-n3-2015-new

2. Нехай тріщини заліковано поблизу внутрішніх вершин:
( , )c b . Подібно до виразів (4), (5)
L = ( c- , )a È ( , )a c , L = ( b- , - ) c È
h
2Eg h 2
p = , (10)
h -
-
p (b c F ( )l
)
)
де l = (b c- )/(b c+ .
Враховуючи, що для новоутвореної конфігурації
)
y = (с a- )/(b a- , (b c- )/ 2 l= (1 - y, l = l (1 - ) (1y + ) l y,
)
0 0 0
та порівнюючи вирази (10) і (9), знайдемо:
-
h F (l )
c = 0 . (11)
1- y F - ( 0 (1 - y ) (1 + l )y )
l
0
3. Нехай тепер колінеарні тріщини заліковані поблизу дальніх вершин:
( , )c b , L =
L = ( b- , - ) c È ( c- , - ) a È ( , )a c . Тоді
h
 2Eg 2 2E g 2 


p = min  0 - , h +  , (12)
h
-
)
  p (c a F ( )l p - ) ( )l  
(c a F
де l = (c a- )/(c a+ .
)
Беручи до уваги, що для цієї конфігурації
y = (b c- )/(b a- , (c a- )/2 l= 0 (1 - y, l = l (1 - ) (1y - 0 ) l y,
)
)
0
із виразів (9), (12) отримаємо:
-  
F (l )  1 h 
c = 0 min  ,  . (13)
1- y   F - ( 0 (1 - y 0 )y )F + ( 0 l - 0 - ) l ) y
(1
) (1y
l
) (1 - l
 
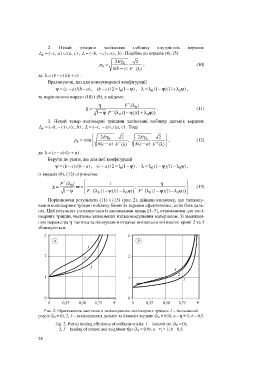
Порівнюючи результати (11) і (13) (рис. 2), дійшли висновку, що залікову-
вання колінеарних тріщин поблизу ближніх вершин ефективніше, аніж біля даль-
ніх. Цей результат узгоджується із висновками праць [1–3], отриманими для колі-
неарних тріщин, частково заповнених низькомодульним матеріалом. Зі зменшен-
ням параметра h тактика заліковування втрачає визначальний вплив: криві 2 та 3
зближуються.

Рис. 2. Ефективність часткового заліковування колінеарних тріщин: 1 – ізольований
розріз (l 0 = 0); 2, 3 – заліковування дальніх та ближніх вершин (l 0 = 0,9); а – h = 1; b – 0,5.
Fig. 2. Partial healing efficiency of collinear cracks: 1 – isolated cut (l 0 = 0);
2, 3 – healing of remote and neighbour tips (l 0 = 0.9); а – h = 1; b – 0.5.
28