Page 24 - Zmist-n3-2015-new

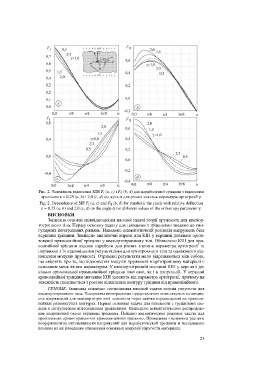
Рис. 2. Залежність відносних КІН F I (a, c) і F II (b, d) для параболічної тріщини з відносним
прогином e = 0,25 (a, b) і 2,0 (c, d) від кута a для різних значень параметра ортотропії g.
Fig. 2. Dependence of SIF F I (a, c) and F II (b, d) for parabolic the crack with relative deflection
e = 0.25 (a, b) and 2.0 (c, d) on the angle a for different values of the orthotropy parameter g.
ВИСНОВКИ
Записано основні співвідношення плоскої задачі теорії пружності для квазіор-
тотропного тіла. Першу основну задачу для площини з тріщинами зведено до син-
гулярних інтегральних рівнянь. Наведено асимптотичний розподіл напружень біля
вершини тріщини. Знайдено аналітичні вирази для КІН у вершині довільно орієн-
тованої прямолінійної тріщини у квазіортотропному тілі. Обчислено КІН для кри-
волінійної тріщини вздовж параболи для різних значень параметра ортотропії та
порівняно з їх відповідними результатами для ортотропного тіла за однакового від-
ношення модулів пружності. Отримані результати мало відрізняються між собою,
що свідчить про те, що відношення модулів пружності в ортотропному матеріалі є
основним механічним параметром. У квазіортотропній площині КІН у вершині до-
вільно орієнтованої прямолінійної тріщини такі самі, як і в ізотропній. У вершині
криволінійної тріщини значення КІН залежать від параметра ортотропії, причому ця
залежність посилюється з ростом відхилення контуру тріщини від прямолінійного.
РЕЗЮМЕ. Записаны основные соотношения плоской задачи теории упругости для
квазиортотропного тела. Построены интегральные представления комплексных потенциа-
лов напряжений для квазиортотропной плоскости через скачки перемещений на криволи-
нейных разомкнутых контурах. Первая основная задача для плоскости с трещинами све-
дена к сингулярным интегральным уравнениям. Приведено асимптотическое распределе-
ние напряжений около вершины трещины. Найдено аналитическое решение задачи для
произвольно ориентированной прямолинейной трещины. Проведены численные расчеты
коэффициентов интенсивности напряжений для параболической трещины и исследовано
влияние на их поведение отношения основных модулей упругости материала.

23