Page 61 - Zmist-n3-2015-new

(рис. 2), тобто прямує до нескінченнос-
ті із наближенням джерела до цієї вер-
-
шини. Натомість його відповідник K
0
q
у лівій вершині та КІНЕЗ K в обох
0
вершинах при l = 1 дорівнюють нулю.
Це означає, що все тепло, виділене дже-
релом безпосередньо біля правого віст-
ря (коли l = 1+0), буде відразу ж повні-
стю стікати поруч (у правій вершині
тріщини (l = 1–0)) і джерело не збурю-
ватиме поля температур у тілі. Тоді не-
¥
обхідно, щоб на нескінченності q = q c.
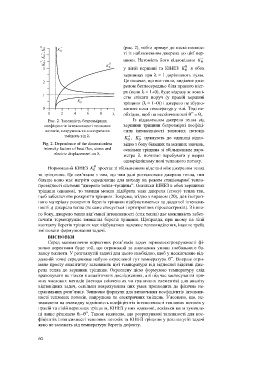
Рис. 2. Залежність безрозмірних Із віддаленням джерела тепла від
коефіцієнтів інтенсивності теплових вершини тріщини безрозмірні коефіці-
потоків, напружень та електричних єнти інтенсивності теплових потоків
зміщень від l. + -
K , K прямують до одиниці відпо-
0 0
Fig. 2. Dependence of the dimensionless відно з боку більших та менших значень,
intensity factors of heat flux, stress and оскільки тріщина зі збільшенням пара-
electric displacement on l. метра l починає перебувати у щораз
одноріднішому полі теплового потоку.
q
Нормований КІНЕЗ K зростає зі збільшенням відстані між джерелом тепла
0
та тріщиною. Це пов’язано з тим, що чим далі розташоване джерело тепла, тим
більше воно має нагріти середовище для виходу на режим стаціонарної тепло-
провідності системи “джерело тепла–тріщина”. Оскільки КІНЕЗ в обох вершинах
тріщини однакові, то завжди можна підібрати знак джерела (стоку) тепла так,
щоб забезпечити розкриття тріщини. Зокрема, згідно з виразом (20), для ізотроп-
ного матеріалу розкриття берегів тріщини відбуватиметься за додатної інтенсив-
ності q джерела тепла (те саме стосується і ортотропних піроелектриків). З іншо-
го боку, джерело тепла від’ємної інтенсивності (стік тепла) дає можливість забез-
печити термопружне змикання берегів тріщини. Щоправда, при цьому на лінії
контакту берегів тріщини має відбуватися належне тепловиділення, інакше треба
змінювати формулювання задачі.
ВИСНОВКИ
Серед математично коректних розв’язків задач термоелектропружності фі-
зично коректним буде той, що отриманий за виконання умови глобального ба-
лансу теплоти. У розглянутій задачі для цього необхідно, щоб у нескінченно від-
¥
даленій точці середовище набуло окресленої тут температури q . Вперше отри-
мано просту аналітичну залежність цієї температури від відносної відстані дже-
рела тепла до вершини тріщини. Окреслену цією формулою температуру слід
враховувати не тільки в аналітичних дослідженнях, а й під час застосування пря-
мих числових методів (методи скінченних чи граничних елементів) для аналізу
відповідних задач, оскільки неврахування цих умов призводить до фізично не-
правильних розв’язків. Записано формули для визначення коефіцієнтів інтенсив-
ності теплових потоків, напружень та електричних зміщень. З’ясовано, що, не-
зважаючи на очевидну відмінність коефіцієнтів інтенсивності теплових потоків у
правій та лівій вершинах тріщини, КІНЕЗ у них однакові, оскільки вони зумовле-
¥
ні лише різницею q c–q . Також виявлено, що розрахункові залежності для кое-
фіцієнтів інтенсивності теплових потоків та КІНЕЗ тріщини у розглянутій задачі
явно не залежать від температури берегів дефекту.

60